Until recently, I didn't know IE (both 6 and 7) had an overflow problem. But it does.

I found it on my personal blog, and my pet project: jQuery for Designers - it's particular visible because I use a lot of code examples.

Here's a detailed account of the problem, and it's fix.

UK EVENTAttend ffconf.org 2024

The conference for people who are passionate about the web. 8 amazing speakers with real human interaction and content you can't just read in a blog post or watch on a tiktok!

The Problem

What I hadn't realised (though kicking myself for not realising earlier) is that IE has a different implementation of overflow compared to Firefox or Safari.

In particular, Firefox et al, when overflowing an element, it puts the horizontal overflow scroll bar on the outside of the element.

You won't notice this difference until you compare to IE:

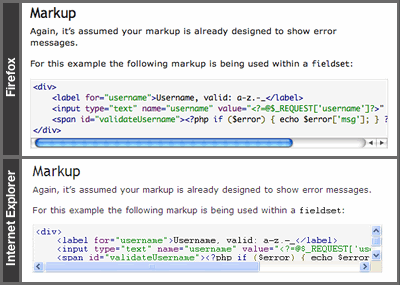
Firefox compared to IE - overflow broken

You'll note that because the content overflows horizontally in IE, the new horizontal scroll bar means we can't see all the content vertically, thus generating a vertical scroll bar.

Here's the worst example, where only one line is overflowed (there's a super tiny vertical scrollbar that you're supposed to use to view the single line):

Worse example of IE overflow

So our aim is to move the horizontal scroll bar to the outside of our overflowed element.

The Solution

It's worth noting that I can only see this being a problem for horizontal overflow. Vertical overflow is always inside the element, and if you have a specific fixed height for your overflowing elements, you'll probably want to skip step (3) below.

So our solution is to apply the following to in IE only:

  1. Find all elements whose contents is overflowing horizontally.
  2. Add 20 pixels of padding to the bottom of our element†.
  3. Strip the vertical scroll bar.

† As far as my testing has seen, the typical height of a scroll bar is 20 pixels.

JavaScript to the Rescue

Disclaimer: As much as I'd love to see this problem solved entirely using CSS, or even the browser doing the job, I can't see how it can be achieved uniformly across all elements, since we only want our changes to apply if, and only if the overflow has occurred (i.e. if we added the padding across the board, some blocks would appear to have an odd blank line when it didn't overflow).

See the working example

window.onload = function () {
  // only apply to IE
  if (!/*@cc_on!@*/0) return;

  // find every element to test
  var all = document.getElementsByTagName('*'), i = all.length;

  // fast reverse loop
  while (i--) {
    // if the scrollWidth (the real width) is greater than
    // the visible width, then apply style changes
    if (all[i].scrollWidth > all[i].offsetWidth) {
      all[i].style['paddingBottom'] = '20px';
      all[i].style['overflowY'] = 'hidden';
    }
  }
};

As a jQuery plugin:

(function ($) {
  $.fn.fixOverflow = function () {
    if ($.browser.msie) {
      return this.each(function () {
        if (this.scrollWidth > this.offsetWidth) {
          $(this).css({ 'padding-bottom' : '20px', 'overflow-y' : 'hidden' });
        }
      });
    } else {
      return this;
    }
  };
})(jQuery);

// usage
$('pre').fixOverflow().doOtherPlugin();

Result

Our JavaScript fix results in IE conforming to putting the horizontal scroll bar below the element:

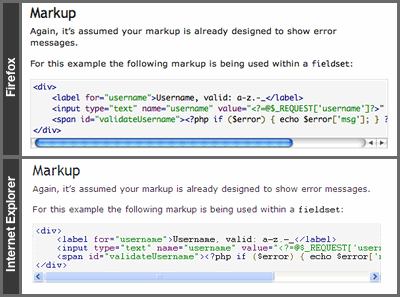
Firefox compared to IE: Overflow fixed

Even better - here's the one line overflow fixed in IE:

One line overflow fixed in IE